Pisagor üçlüsü
Bu maddede kaynak listesi bulunmasına karşın metin içi kaynakların yetersizliği nedeniyle bazı bilgilerin hangi kaynaktan alındığı belirsizdir. (Haziran 2016) (Bu şablonun nasıl ve ne zaman kaldırılması gerektiğini öğrenin) |
Pisagor üçlüsü, a2+b2=c2 eşitliğini sağlayan a, b,c tam sayılarına verilen addır. Örneğin (3,4,5) bir Pisagor üçlüsüdür. Eğer herhangi bir (a, b,c) Pisagor üçlüsüyse (ka, kb, kc) de bir Pisagor üçlüsüdür. Eğer (a, b,c) aralarında asalsa buna temel Pisagor üçlüsü denir.
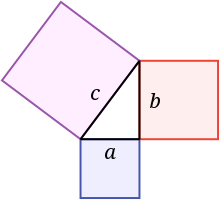
Pisagor üçlüleri bir dik üçgenin kenarlarını oluşturduğu için Pisagor teoremi'ne atıf olarak bu isimle adlandırılır. Ancak her dik üçgenin kenar uzunlukları Pisagor üçlüsü değildir. Örneğin (1,1,√2) üçgeninde √2 tam sayı olmadığı için bu bir Pisagor üçlüsü değildir.
Örnekler
değiştirc ≤ 100 şartını sağlayan 16 tane temel Pisagor üçlüsü vardır:
| (3, 4, 5 ) | (5, 12, 13) | (7, 24, 25) | (8, 15, 17) |
| (9, 40, 41) | (11, 60, 61) | (12, 35, 37) | (13, 84, 85) |
| (16, 63, 65) | (20, 21, 29) | (28, 45, 53) | (33, 56, 65) |
| (36, 77, 85) | (39, 80, 89) | (48, 55, 73) | (65, 72, 97) |
100 < c ≤ 300 şartını sağlayan temel Pisagor üçlüleri:
| (20, 99, 101) | (60, 91, 109) | (15, 112, 113) | (44, 117, 125) |
| (88, 105, 137) | (17, 144, 145) | (24, 143, 145) | (51, 140, 149) |
| (85, 132, 157) | (119, 120, 169) | (52, 165, 173) | (19, 180, 181) |
| (57, 176, 185) | (104, 153, 185) | (95, 168, 193) | (28, 195, 197) |
| (84, 187, 205) | (133, 156, 205) | (21, 220, 221) | (140, 171, 221) |
| (60, 221, 229) | (105, 208, 233) | (120, 209, 241) | (32, 255, 257) |
| (23, 264, 265) | (96, 247, 265) | (69, 260, 269) | (115, 252, 277) |
| (160, 231, 281) | (161, 240, 289) | (68, 285, 293) |
Kaynakça
değiştir- Şafak Alpay. "Pisagor Üçlüleri". Matematik Dünyası. 26 Mart 2023 tarihinde kaynağından arşivlendi.
| Geometri ile ilgili bu madde taslak seviyesindedir. Madde içeriğini genişleterek Vikipedi'ye katkı sağlayabilirsiniz. |