Renormalizasyon (fizik)
Kuantum alan teorisinde, renormalizasyon veya yeniden normalleştirme, pertürbatif genişlemede hesaplanan miktarda ortaya çıkan sonsuzlukların bir dizi teknik kullanılarak giderilmesi süreci.
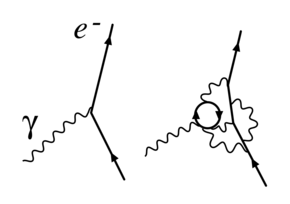
Kuantum alan teorisinde, fotonlardan, pozitronlardan ve diğer ufak parçacıklardan oluşan bir sanal parçacık bulutu, başlangıçtaki elektronu çevreler ve onunla etkileşir. Çevredeki parçacıkların birbiriyle etkileşimlerinin muhasebeleştirilmesi, elektron sisteminin başlangıçta tahmin edilenden daha farklı bir kütleye ve yüke sahipmiş gibi davrandığını gösterir. Bu örnekte renormalizasyon bir elektronun başlangıçta öngörülen kütlesini ve yükünü matematiksel ve deneysel olarak gözlemlenen kütle ve yük ile değiştirir. Matematiksel deneyler, pozitronların ve protonlar gibi büyük parçacıkların çok daha güçlü etkileşimlerin ve daha yoğun sanal parçacık bulutlarının varlığında bile, elektronla aynı gözlenen yükü gösterdiğini ispatlamaktadır.
Uzay-zamanı bir süreklilik olarak tanımlarken, bazı istatistiksel ve kuantum mekaniksel yapılar iyi tanımlanmamıştır. Bunları tanımlamak veya açık hale getirmek için bir süreklilik sınırı, çeşitli ölçeklerdeki kafeslerin "yapı iskelesini" dikkatlice kaldırmalıdır. Renormalizasyon prosedürleri, belirli fiziksel miktarların—bir elektronun kütlesi ve yükü gibi—gözlemlenen ve test edilenbilen değerlere eşit olması gereksinimine dayanır. Yani, fiziksel niceliğin deneysel değeri uygulanabilirlik sağlar, ancak deneysel doğası nedeniyle gözlemlenen ölçüm, kuantum alan teorisinin teorik tabanlardan daha derin türevler gerektiren alanlarını temsil eder.
Renormalizasyon ilk önce pertürbasyon teorisinde sonsuz integralleri anlamak için kuantum elektrodinamiğinde (KED'de) geliştirilmiştir. Başlangıçta bazı yaratıcıları tarafından bile şüpheli geçici bir prosedür olarak görülen renormalizasyon, sonunda fizik ve matematiğin çeşitli alanlarında önemli ve kendi kendine tutarlı bir ölçek fiziği mekanizması olarak benimsenmiştir.
Klasik fizikte ki öz-etkileşimler
değiştirSonsuzluk problemi ilk olarak 20. yüzyılın başlarında, temel parçacıkların klasik elektrodinamiği üzerine yapılan çalışmalar sonucunda ortaya çıktı. Yüklü bir parçacığın kütlesi, elektrostatik alanındaki (elektromanyetik kütle) kütle enerjisini içermelidir. Parçacık yarıçapının re yüklü bir küresel kabuğu olduğunu varsayalım; alandaki kütle–enerji:
re → 0 olarak sonsuz hale gelir. Bu, noktasal parçacığın sonsuz eylemsizliğe sahip olacağı anlamına gelir ve bu da onu hızlandırılamaz hale getirir. Burada 'nin elektron kütlesine eşit olmasını sağlayan re'nin değerine klasik elektron yarıçapı denir.
burada ince yapı sabiti ve ise elektronun Compton dalga boyudur.