Log-normal dağılım

Olasılık kuramı ve istatistik bilim dallarında log-normal dağılım logaritması normal dağılım gösteren herhangi bir rassal değişken için tek-kuyruklu bir olasılık dağılımdır. Eğer Y normal dağılım gösteren bir rassal değişken ise, bu halde X= exp(Y) için olasılık dağılımı bir log-normal dağılımdır; aynı şekilde eğer X log-normal dağılım gösterirse o halde log(X) normal dağılım gösterir. Logaritma fonksiyonu için bazın ne olduğu önemli değildir: Herhangi iki pozitif sayı olan a, b ≠ 1 için eğer log_a(X) normal dağılım gösterirse, log_b(X) fonksiyonu da normaldir.

Log-normal

Olasılık yoğunluk fonksiyonu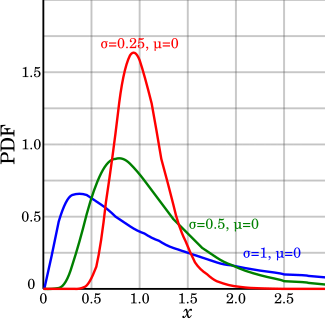 μ=0
Yığmalı dağılım fonksiyonu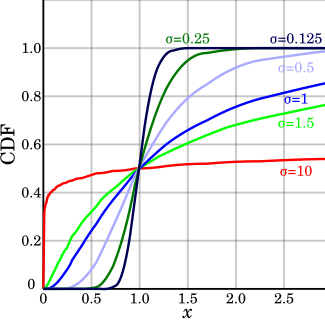 μ=0
Parametreler	$\sigma >0$ $-\infty <\mu <\infty$
Destek	$[0,+\infty )\!$
Olasılık yoğunluk fonksiyonu (OYF)	${\frac {1}{x\sigma {\sqrt {2\pi }}}}\exp \left[-{\frac {\left(\ln(x)-\mu \right)^{2}}{2\sigma ^{2}}}\right]$
Birikimli dağılım fonksiyonu (YDF)	${\frac {1}{2}}+{\frac {1}{2}}\mathrm {erf} \left[{\frac {\ln(x)-\mu }{\sigma {\sqrt {2}}}}\right]$
Ortalama	$e^{\mu +\sigma ^{2}/2}$
Medyan	$e^{\mu }\,$
Mod	$e^{\mu -\sigma ^{2}}$
Varyans	$(e^{\sigma ^{2}}\!\!-1)e^{2\mu +\sigma ^{2}}$
Çarpıklık	$(e^{\sigma ^{2}}\!\!+2){\sqrt {e^{\sigma ^{2}}\!\!-1}}$
Fazladan basıklık	${e^{4\sigma ^{2}}+2e^{3\sigma ^{2}}+3e^{2\sigma ^{2}}-6}$
Entropi	${\frac {1}{2}}+{\frac {1}{2}}\ln(2\pi \sigma ^{2})+\mu$
Moment üreten fonksiyon (mf)	(Ham momentler için metine bakin)
Karakteristik fonksiyon

Karakterizasyon

Olasılık yoğunluk fonksiyonu

Log-normal dağılım için olasılık yoğunluk fonksiyonu $x>0$ için şudur:

$f(x;\mu ,\sigma )={\frac {1}{x\sigma {\sqrt {2\pi }}}}e^{-{\frac {(\ln(x)-\mu )^{2}}{2\sigma ^{2}}}}$

Burada μ ve σ değişkenin logaritma değerleri için ortalama ve standart sapmasidir. Bu halde parametreler kullanılan logaritma türünde (ya e bazlı, 2 bazlı veya 10 bazlı) birimlerdedir. Ancak radyo komünikasyon incelemelerinde bu parametreler tipik olarak desibel birimleri iledir.

Yığmalı dağılım fonksiyonu

Log-normal dağılım için yığmalı dağılım fonksiyonu şudur:

${\frac {1}{2}}+{\frac {1}{2}}\mathrm {erf} \left[{\frac {\ln(x)-\mu }{\sigma {\sqrt {2}}}}\right]$

Momentler

Bütün momentler şu ifadelerle verilmiştir:

$\mu _{k}=e^{k\mu +k^{2}\sigma ^{2}/2}.$

Moment üreten fonksiyon

Log-normal dağılım için moment ureten fonksiyon bulunmamaktadır.

Özellikler

Ortalama ve standart sapma

Beklenen değer (ortalama) şudur:

$\mathrm {E} (X)=e^{\mu +\sigma ^{2}/2}\,\!$

Varyans şöyle ifade edilir:

$\mathrm {Var} (X)=(e^{\sigma ^{2}}-1)e^{2\mu +\sigma ^{2}}\,\!$

ve standart sapma şu olur:

$\mathrm {StdDev} (X)={\sqrt {\mathrm {Var} (X)}}={\sqrt {(e^{\sigma ^{2}}-1)}}e^{\mu +\sigma ^{2}/2}\,\!$

Beklenen değer ve varyans verilmiş olduğu halde μ ve σ² değerlerini elde etmek için kullanılan bağlantılar şöyle ifade edilir:

$\mu =\ln(\mathrm {E} (X))-{\frac {1}{2}}\ln \left(1+{\frac {\mathrm {Var} (X)}{(\mathrm {E} (X))^{2}}}\right)\,\!$

$\sigma ^{2}=\ln \left({\frac {\mathrm {Var} (X)}{(\mathrm {E} (X))^{2}}}+1\right)\,\!$

Mod ve medyan

Bu dağılım için mod şudur:

$\mathrm {Mode} (X)=e^{\mu -\sigma ^{2}}\,\!$

Medyan şudur:

${\tilde {X}}=e^{\mu }\,\!$

Geometrik ortalama ve geometrik standart sapma

Log-normal dağılım için geometrik ortalama $e^{\mu }\,\!$ ve geometrik standart sapma $e^{\sigma }\,\!$ olur.

Eğer bir örneklem veri serisi log-normal dağılım gösteren bir anakütleden gelmişse, geometrik ortalama ve geometrik standart sapma güvenlilik aralık kestirimi elde etmek için kullanılabilir. Bu noramal dağılım gösteren anakütleden gelen örneklem verilerinden aritmetik ortalama ve standart sapma kullanılarak güvenlilik aralığı bulmaya benzemektedir.

Güvenlik aralığı sınırları	Log uzayi	Geometrik
3σ alt sınır	$\mu -3\sigma \,\!$	$\mu _{\mathrm {geo} }/\sigma _{\mathrm {geo} }^{3}\,\!$
2σ alt sınır	$\mu -2\sigma \,\!$	$\mu _{\mathrm {geo} }/\sigma _{\mathrm {geo} }^{2}\,\!$
1σ alt sınır	$\mu -\sigma \,\!$	$\mu _{\mathrm {geo} }/\sigma _{\mathrm {geo} }\,\!$
1σ üst sınır	$\mu +\sigma \,\!$	$\mu _{\mathrm {geo} }\sigma _{\mathrm {geo} }\,\!$
2σ üst sınır	$\mu +2\sigma \,\!$	$\mu _{\mathrm {geo} }\sigma _{\mathrm {geo} }^{2}\,\!$
3σ üst sınır	$\mu +3\sigma \,\!$	$\mu _{\mathrm {geo} }\sigma _{\mathrm {geo} }^{3}\,\!$

Burada geometrik ortalama $\mu _{\mathrm {geo} }=\exp(\mu )\,\!$ ve geometrik standart sapma $\sigma _{\mathrm {geo} }=\exp(\sigma )\,\!$ olur.

Momentler

Bu dağılım için ilk birkaç ham momentler şunlardır:

$\mu _{1}=e^{\mu +\sigma ^{2}/2}\,\!$

$\mu _{2}=e^{2\mu +4\sigma ^{2}/2}\,\!$

$\mu _{3}=e^{3\mu +9\sigma ^{2}/2}\,\!$

$\mu _{4}=e^{4\mu +16\sigma ^{2}/2}\,\!$

$\mu _{k}=e^{k\mu +k^{2}\sigma ^{2}/2}\,\!$

İlişkili dağılımlar

• Eğer $X\sim N(\mu ,\sigma ^{2})$ bir normal dağılım gösterirse, o halde $\exp(X)\sim \operatorname {Log-N} (\mu ,\sigma ^{2})$.
• Eğer $X_{m}\sim \operatorname {Log-N} (\mu _{m},\sigma _{m}^{2}),\ m={1,...,n}\$ bağımsız olarak parametreleri aynı μ ve değişik σ olan log-normal dağılım gösteren değişkenlerse ve $Y=\prod _{m=1}^{n}X_{m}$ ise, o halde Y de log-normal dağılım gösteren değişkendir; yani $Y\sim \operatorname {Log-N} \left(n\mu ,\sum _{m=1}^{n}\sigma _{m}^{2}\right)$ olur.

Ayrıca bakınız

• Normal dağılım
• Geometrik ortalama

Kaynakça

• Aitchison, J. and Brown, J.A.C. (1957), The Lognormal Distribution,
• Brooks,R., Corson,J. ve Wales,J.D, (1994), "The Pricing of Index Options When the Underlying Assets All Follow a Lognormal Diffusion" 22 Haziran 2008 tarihinde Wayback Machine sitesinde arşivlendi., Advances in Futures and Options Research, C7
• Hull, J. (2005), "Properties of Lognormal Distribution" Options, Futures, and Other Derivatives 6ed'
• Lee,C.F. ve Lee, J. C. (to appear) "Normal and Lognormal Distribution" Alternative Option Pricing Models: Theory, Methods, and Applications 27 Eylül 2007 tarihinde Wayback Machine sitesinde arşivlendi., Kluwer Academic Publishers
• Limpert,M., Stahel,W. ve Abbt,M., (2001) "Log-normal Distributions across the Sciences: Keys and Clues" 19 Nisan 2008 tarihinde Wayback Machine sitesinde arşivlendi., BioScience, C.51 No.5 say. 341-352
• Swamee,P.K. (2002), "Near Lognormal Distribution", Journal of Hydrologic Engineering, C7 No.6 say.441-444
• Weisstein, E.W. et al. (2006) "Log Normal Distribution" 12 Temmuz 2008 tarihinde Wayback Machine sitesinde arşivlendi. 26 Ekim 2006.