Bilineer interpolasyon , lineer interpolasyonun iki değişkenli fonksiyonların (ör. x ve y ) rectilineer iki-boyutlu grid üzerinde interpolasyonu için olan uzantısıdır.
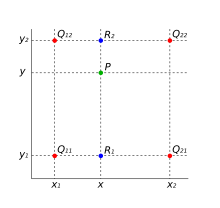
Dört kırmızı nokta eldeki datayı ve yeşil nokta da interpolasyon yapılacak noktayı göstermektedir. Metot, lineer interpolasyonun önce bir yönde sonra diğer yönde sırasıyla uygulanmasına dayanır. Bu iki adım kendi içinde lineerse de, metot, bir bütün olarak lineer değil; quadratic tir.
Bilinmeyen bir fonksiyon f 'in (x, y ) noktasındaki değerinin bulunacağı varsayılsın. Ayrıca, f 'in dört noktadaki değeri bilinsin: Q 11 = (x 1 , y 1 ), Q 12 = (x 1 , y 2 ), Q 21 = (x 2 , y 1 ) ve Q 22 = (x 2 , y 2 ).
İlk olarak, x -doğrultusunda lineer interpolasyon aşağıdaki gibi yapılır:
f
(
x
,
y
1
)
≈
x
2
−
x
x
2
−
x
1
f
(
Q
11
)
+
x
−
x
1
x
2
−
x
1
f
(
Q
21
)
f
(
x
,
y
2
)
≈
x
2
−
x
x
2
−
x
1
f
(
Q
12
)
+
x
−
x
1
x
2
−
x
1
f
(
Q
22
)
{\displaystyle {\begin{aligned}f(x,y_{1})&\approx {\frac {x_{2}-x}{x_{2}-x_{1}}}f(Q_{11})+{\frac {x-x_{1}}{x_{2}-x_{1}}}f(Q_{21})\\f(x,y_{2})&\approx {\frac {x_{2}-x}{x_{2}-x_{1}}}f(Q_{12})+{\frac {x-x_{1}}{x_{2}-x_{1}}}f(Q_{22})\end{aligned}}}
İkinci olarak, yukarıdaki denklem, y -doğrultusunda lineer interpolasyonu uygulanırsa, aşağıdaki denklem bulunur:
f
(
x
,
y
)
≈
y
2
−
y
y
2
−
y
1
f
(
x
,
y
1
)
+
y
−
y
1
y
2
−
y
1
f
(
x
,
y
2
)
≈
y
2
−
y
y
2
−
y
1
(
x
2
−
x
x
2
−
x
1
f
(
Q
11
)
+
x
−
x
1
x
2
−
x
1
f
(
Q
21
)
)
+
y
−
y
1
y
2
−
y
1
(
x
2
−
x
x
2
−
x
1
f
(
Q
12
)
+
x
−
x
1
x
2
−
x
1
f
(
Q
22
)
)
=
1
(
x
2
−
x
1
)
(
y
2
−
y
1
)
(
f
(
Q
11
)
(
x
2
−
x
)
(
y
2
−
y
)
+
f
(
Q
21
)
(
x
−
x
1
)
(
y
2
−
y
)
+
f
(
Q
12
)
(
x
2
−
x
)
(
y
−
y
1
)
+
f
(
Q
22
)
(
x
−
x
1
)
(
y
−
y
1
)
)
=
1
(
x
2
−
x
1
)
(
y
2
−
y
1
)
[
x
2
−
x
x
−
x
1
]
[
f
(
Q
11
)
f
(
Q
12
)
f
(
Q
21
)
f
(
Q
22
)
]
[
y
2
−
y
y
−
y
1
]
{\displaystyle {\begin{aligned}f(x,y)&\approx {\frac {y_{2}-y}{y_{2}-y_{1}}}f(x,y_{1})+{\frac {y-y_{1}}{y_{2}-y_{1}}}f(x,y_{2})\\&\approx {\frac {y_{2}-y}{y_{2}-y_{1}}}\left({\frac {x_{2}-x}{x_{2}-x_{1}}}f(Q_{11})+{\frac {x-x_{1}}{x_{2}-x_{1}}}f(Q_{21})\right)+{\frac {y-y_{1}}{y_{2}-y_{1}}}\left({\frac {x_{2}-x}{x_{2}-x_{1}}}f(Q_{12})+{\frac {x-x_{1}}{x_{2}-x_{1}}}f(Q_{22})\right)\\&={\frac {1}{(x_{2}-x_{1})(y_{2}-y_{1})}}\left(f(Q_{11})(x_{2}-x)(y_{2}-y)+f(Q_{21})(x-x_{1})(y_{2}-y)+f(Q_{12})(x_{2}-x)(y-y_{1})+f(Q_{22})(x-x_{1})(y-y_{1})\right)\\&={\frac {1}{(x_{2}-x_{1})(y_{2}-y_{1})}}{\begin{bmatrix}x_{2}-x&x-x_{1}\end{bmatrix}}{\begin{bmatrix}f(Q_{11})&f(Q_{12})\\f(Q_{21})&f(Q_{22})\end{bmatrix}}{\begin{bmatrix}y_{2}-y\\y-y_{1}\end{bmatrix}}\end{aligned}}}
Birim bir kare üzerindeki bir bilineer interpolasyonu örneği. z-değerleri 0, 1, 1 ve 0.5'tir. İnterpolasyon değerleri renkle gösterilmiştir. Son denklem, hangi doğrultu ile başlanırsa başlansın, aynıdır. Örneğin, önce y- sonra x- doğrultusunda yapılan iki ardışık lineer interpolasyon yukarıdaki aynı terimi verir.
İnterpolasyonun ifadesinde alternatif bir yöntem aşağıdaki gibidir:
f
(
x
,
y
)
≈
a
0
+
a
1
x
+
a
2
y
+
a
3
x
y
{\displaystyle f(x,y)\approx a_{0}+a_{1}x+a_{2}y+a_{3}xy}
Denklemin katsayıları aşağıdaki lineer sistemin çözülmesi ile elde edilir:
[
1
x
1
y
1
x
1
y
1
1
x
1
y
2
x
1
y
2
1
x
2
y
1
x
2
y
1
1
x
2
y
2
x
2
y
2
]
[
a
0
a
1
a
2
a
3
]
=
[
f
(
Q
11
)
f
(
Q
12
)
f
(
Q
21
)
f
(
Q
22
)
]
{\displaystyle {\begin{aligned}{\begin{bmatrix}1&x_{1}&y_{1}&x_{1}y_{1}\\1&x_{1}&y_{2}&x_{1}y_{2}\\1&x_{2}&y_{1}&x_{2}y_{1}\\1&x_{2}&y_{2}&x_{2}y_{2}\end{bmatrix}}{\begin{bmatrix}a_{0}\\a_{1}\\a_{2}\\a_{3}\end{bmatrix}}={\begin{bmatrix}f(Q_{11})\\f(Q_{12})\\f(Q_{21})\\f(Q_{22})\end{bmatrix}}\end{aligned}}}
Eğer çözüm f(Q) cinsinden istenirse, aşağıdaki ifade kullanılabilir:
f
(
x
,
y
)
≈
b
11
f
(
Q
11
)
+
b
12
f
(
Q
12
)
+
b
21
f
(
Q
21
)
+
b
22
f
(
Q
22
)
{\displaystyle f(x,y)\approx b_{11}f(Q_{11})+b_{12}f(Q_{12})+b_{21}f(Q_{21})+b_{22}f(Q_{22})}
Bu denklemin katsayıları da aşağıdaki sistemin çözümüyle elde edilir:
[
b
11
b
12
b
21
b
22
]
=
(
[
1
x
1
y
1
x
1
y
1
1
x
1
y
2
x
1
y
2
1
x
2
y
1
x
2
y
1
1
x
2
y
2
x
2
y
2
]
−
1
)
T
[
1
x
y
x
y
]
{\displaystyle {\begin{bmatrix}b_{11}\\b_{12}\\b_{21}\\b_{22}\end{bmatrix}}=\left({\begin{bmatrix}1&x_{1}&y_{1}&x_{1}y_{1}\\1&x_{1}&y_{2}&x_{1}y_{2}\\1&x_{2}&y_{1}&x_{2}y_{1}\\1&x_{2}&y_{2}&x_{2}y_{2}\end{bmatrix}}^{-1}\right)^{T}{\begin{bmatrix}1\\x\\y\\xy\end{bmatrix}}}
Eğer f 'in bilindiği dört noktanın koordinatları (0, 0), (0, 1), (1, 0) ve (1, 1), ise; interpolasyon denklemi aşağıdakince sadeleşir:
f
(
x
,
y
)
≈
f
(
0
,
0
)
(
1
−
x
)
(
1
−
y
)
+
f
(
1
,
0
)
x
(
1
−
y
)
+
f
(
0
,
1
)
(
1
−
x
)
y
+
f
(
1
,
1
)
x
y
.
{\displaystyle f(x,y)\approx f(0,0)(1-x)(1-y)+f(1,0)x(1-y)+f(0,1)(1-x)y+f(1,1)xy.}
Eşdeğer matris formatında ise denklem:
f
(
x
,
y
)
≈
[
1
−
x
x
]
[
f
(
0
,
0
)
f
(
0
,
1
)
f
(
1
,
0
)
f
(
1
,
1
)
]
[
1
−
y
y
]
.
{\displaystyle f(x,y)\approx {\begin{bmatrix}1-x&x\end{bmatrix}}{\begin{bmatrix}f(0,0)&f(0,1)\\f(1,0)&f(1,1)\end{bmatrix}}{\begin{bmatrix}1-y\\y\end{bmatrix}}.}